
How we solve problems is the most important knowledge learned in math.
I believe that as a facilitator, I need to set aside plenty of time for the learner to build up the knowledge for how to solve a problem. In my math club, I would bring 5 problems to solve each week. The first month, learners may get through 1-2 problems. The third month, learners may get through 3 problems. It takes about 6 months to get most learners to solve 4-5 multi-step problems in under 30 minutes. Problem solving is worth knowing and worth the time investment and there are no shortcuts. It takes constant trying and reflecting on the part of the learner to build up the knowledge for how to solve a problem effectively.
I believe it is important for the teacher to have the knowledge that the strategies used to solve a problem and how we solve a problem are two separate entities of knowledge. Too often I see the two intermingled.
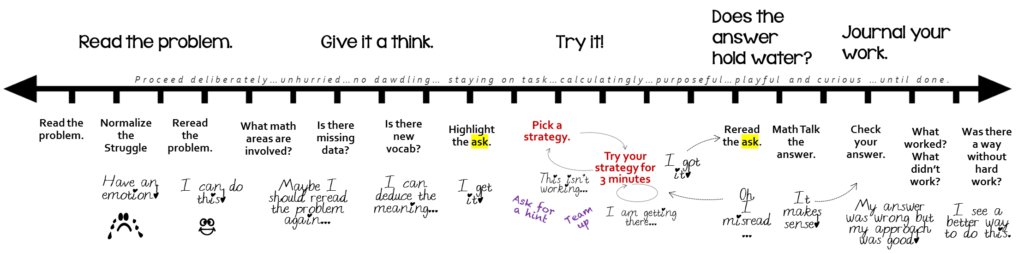
Figure 4: A Problem-Solving Timeline
The art of solving a problem is a mix of knowledge, from slowing down when reading a problem, recognizing emerging emotions and frustrations and not letting them get the better of you, rereading the problem looking for vocabulary words you are unsure of and possible missing data, looking for patterns that hint at what strategies might be useful to solve the problem, just doing it, and then thinking and using math talk to prove to yourself and your classmates whether the answer that you arrived at holds water and if your strategy makes sense. It ends with reflection – looking at the actual answer in comparison to what you arrived at, and thinking about what worked and what didn’t work. Looking at others’ approaches for potentially faster methods and trying the problem a second time.
On the other hand, the knowledge of a set of strategies to be used in solving the problem is built out over time by the learner. Like a carpenter builds out his tool chest, a learner builds out his tool set by adding methods that they learn over time. I believe in keeping a “How Will You Solve it?” Chart up, and letting the learners define what methods go on it from their experiences. Each learner is unique and will be comfortable with their strategies. That one way requires less hard work will drive the learner to strive for higher-order strategies. The learner cannot move to higher-order (i.e. more abstract) strategies without putting in the time building knowledge of the low-order (i.e. more physical) strategies. There are no shortcuts.

Mental math and number sense are worth knowing at the elementary level.
The philosophy behind mental math is that students should know how to solve problems in one’s head without the help of a pencil, paper or calculator. Number sense is the ability of a learner to use their understanding of numbers to solve operations and problems in dexterous ways. Number sense and mental math both provide a set of practical skills that helps a learner solve problems with speed and accuracy. They take the drudgery out of solving complex math problems and pave the way for a deeper understanding of mathematics.
Having a strong sense of numbers, a learner can surface relationships and patterns that exist in numbers. A learner can look at the number 16, for example and when solving a problem, he will see the number 16 in many incarnations. Two sets of eight, fifteen plus one, 42, 1016,10000binary, one ten and six ones, ten and six, a dime, a nickel and a penny… having this knowledge will enable the learner to adroitly apply the best representation to meet the demands of the problem.

To perform math mentally, without pencil and paper, requires the knowledge of a new set of approaches to addition and multiplication. For example, using mental math, we can calculate 11×36 by reordering how we multiply, and see the answer as 396 without giving it a second of thought.
These skills encourage a deeper understanding of numbers, are practical and will take some of the hard work out of math in later years. It is proven that learners knowing number sense and mental math become faster and more adept with problem solving. Learners with this knowledge will more likely be confident and successful in advanced math in later years.
Math Talk enables learners to build thinking and reasoning in math.

Classroom discussions are commonly associated with reading and lab. Only centuries ago, math was all prose and step-by-step manuals, describing in simple language how a problem could be solved (Note symbols and functions did not take root until the early 18th century.) Now it has become common to teach first in symbols and functions, and then retrace what was learned using nouns and verbs only to ensure the children can speak to what they have learned. This all seems a little bit backwards.
Knowing how to use Math Talk provides the learner with the structured tools they need to surface patterns, identify strategies, reason and collaborate. (Chapin, 2009) It also helps teachers surface any learner misunderstandings and missed precursors. It ensures understanding in parallel with the application of symbols and functions.
Vocabulary is not just the domain of language Arts.
Vocabulary is foundational to math, as we examine a problem to understand which words are hints to how to solve the problem. The sometimes-complex conventions applied to math terms alone call for us to actively examine definitions and word ingredients (e.g. Greatest Common Factor, Hexagon Based Prism). And on occasion we create rules that make more sense to the classroom (e.g. A prime number is measured by a unit alone.) rather than the complicated ones in the textbook. The knowledge of math vocabulary is a big part to a learner’s ability to solving a real problem.
Simple terms like congruent (i.e. the same size) and counting numbers (1, 2, 3, …) can lead to wrong answers when not remembered or misunderstood. Words that seem so complicated, like octagon-based prism, are easy when can spot their word parts.
I believe that a part of the math day is spent on math vocabulary and multi-modal techniques, like those employed by Membean (membean.com) for language arts, in the math classroom.
Learning other number systems helps us better understand our number system by giving us something to contrast it with.
Learning other number systems is important because we build knowledge best when we are curious. We begin to better understand what we have when we have something to contrast it with.
Each year there is a global Math day hosted by the Student Research foundation and one big mathematical experience is shared by learners across the globe. In past years, it has centered around learning number systems other than the decimal system. It was through this effort that I learned about the impact that learning other number systems such as binary and Roman Numerals was having on learners. By exploring a number system other than our own Hindu-Arabic decimal system, the learners know had something to contrast it with. That Roman Numerals do not have a concept of zero or place value. That binary only has 2 numbers to count with (i.e. 0 and 1) versus our system that has 10 (i.e. 0…9). The students so enjoyed the knowledge gained and transformed the school floor to the new systems learned.
Visual spatial skills, prime numbers and cryptarithms round out the knowledge needed for a learner to have a successful math outcome.
I believe crucial to rounding out the knowledge of a learner in math include visual spatial skills, important to a learner being able to mentally manipulate a problem; there is a direct impact on this knowledge and a learners’ ability to work at an abstract level.
Prime numbers should be learned deeply, the rules to identifying a prime under 100 are so easy to learn, and there are only 25 of them to memorize. Doing so removes much of the hard work associated with factoring numbers at the elementary level and beyond.
Cryptarithms are mathematical puzzles, that often come up in math competitions, where the digits in a sum have been replaced by letters. They challenge learners to work systematically and help to build a better understanding of place value.
See figure 5 for a complete picture of what is worth knowing at the elementary level.
