The purpose of this article is to provide an introduction to parents and caregivers on the importance of learning prime numbers, including: What is a prime number, why they are important, and what you can do to help your child achieve a good outcome in math.

As you were working on your multiplication tables, did you notice that some numbers like 12 came up again and again (i.e. 3X4, 6X2, 1X12), while others like 11 only came up once (i.e. 1X11).
This concept has fascinated mathematicians since the time of the ancient Greeks. This is the concept behind prime numbers and composite numbers.
There are no patterns known that can help us to determine where the next prime number will come up in a sequence of numbers.
There are, however, strategies that can help us more quickly figure out if a number is or isn’t prime.

What is a Prime Number?
The number 1 is not a prime.
The first prime number is 2.
2 is a special number in the prime world;
2 is the only even prime.
It’s quickly followed by prime numbers:
3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41,
43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97 and so on…
Prime numbers have only two factors, 1 and itself.
For example, 5 has only 2 factors, 1 and 5, so it is a prime.
6 has more than 2 factors (1 and 6, 2 and 3) so
it is not prime.
A composite number is the antonym of a prime number, and has more than two factors.
For example, 12 has more than 2 factors other than 1 and itself (3 and 4, 2 and 6), so it is a composite number.
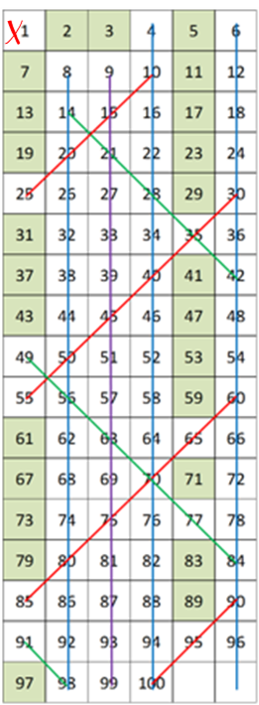
All numbers are either prime or composite… with one exception… the number 1. Number 1 was once a prime but was demoted by the mathematical community
(see video: Why 1 is Not a Prime).
Why are Prime Numbers Important?
Just as there are an infinite amount of numbers, there are an infinite amount of prime numbers. Primes become less frequent as numbers grow larger, but there is always another prime number, you just don’t know when the next one will appear numerically.
Mathematicians are forever looking for a strategy to identify very big prime numbers. The best mathematicians have chewed on this problem for thousands of years with no success.
It is hard to figure out whether a very big number is a prime. It’s one thing to figure out the prime factors of 20, and quite another to find the prime factors of 2,244,354 (2 X 3 X 7 X 53,437). It’s quite another to find the prime factors of a number that is fifty digits long.
That fact makes prime numbers vitally important to encryption. Cryptography mostly works based on the difficulty in finding a large prime number. If ever a new mathematical strategy could lead to finding primes quickly and easily, it would break all encryption as we know it.
But Really… Why are Primes Important?
I struggle to find any practical use for prime numbers beyond encryption and that they represent the atoms of our number system. But… I have to wonder…
We have been playing with primes since at least 300 B.C. because we are curious. Yet an applied use for prime numbers only came up in the 1970’s (i.e. after the invention of cryptographic algorithms like RSA).
But isn’t that how Mathematics works? Mathematics is a constant pull and tug between pure mathematics and applied mathematics; pure means that we play with math because it is intriguing and we are curious, and applied means that we use that play to solve everyday problems.
I like to believe that our continued curiosity in primes is a sign that there may be more important applications of prime numbers to come.
“Give us more practical uses,” you ask? Primes come up an awful lot in math contests and in middle-school math. Prime are, after all, the building blocks of numbers. Primes are to numbers as atoms are to molecules. Therefor, many areas of math depend on a good grasp of primes, including factoring and simplifying fractions. Improving your sense of prime numbers will enable you to answer these problems with greater speed and accuracy.
And for those shooting for the stars… Truly the great questions are still open in the field of mathematics as they relate to prime numbers — How do you more quickly find the very big prime numbers? As of May 2017, 274,207,281-1 is the largest known prime number, a very small number when we are looking to infinity for primes. How do you find very big prime pairs? Solve these problems and you can earn your place in the history books!
What Should I Do?
Help your child build a sense of what is a prime number and what is composite.

We do this through simple memorization of the lower primes, using stories, sieves, pictures and tables to familiarize ourselves with prime numbers up to 100 (i.e. there are only 25), and
by learning strategies that help us to more quickly identify the larger primes. There is even an App (Ninja Chicken) and a web prime game to help.
Thank You!
We at NJ Loves Math so much appreciate your taking the time to read this article. Please feel comfortable to provide any feedback as to its usefulness.
References
Geek Answers: Why should we care about prime numbers? (2013, October 27). Retrieved from http://www.geek.com/news/geek-answers-why-should-we-care-about-prime-numbers-1574269/.
Glenn Westmore: Prime Numbers. (2013, October 27). Retrieved from from http://www.glennwestmore.com.au/category/prime-numbers/.
Ellison, G. (2013). Hard math for elementary school. North Charleston, SC: CreateSpace.